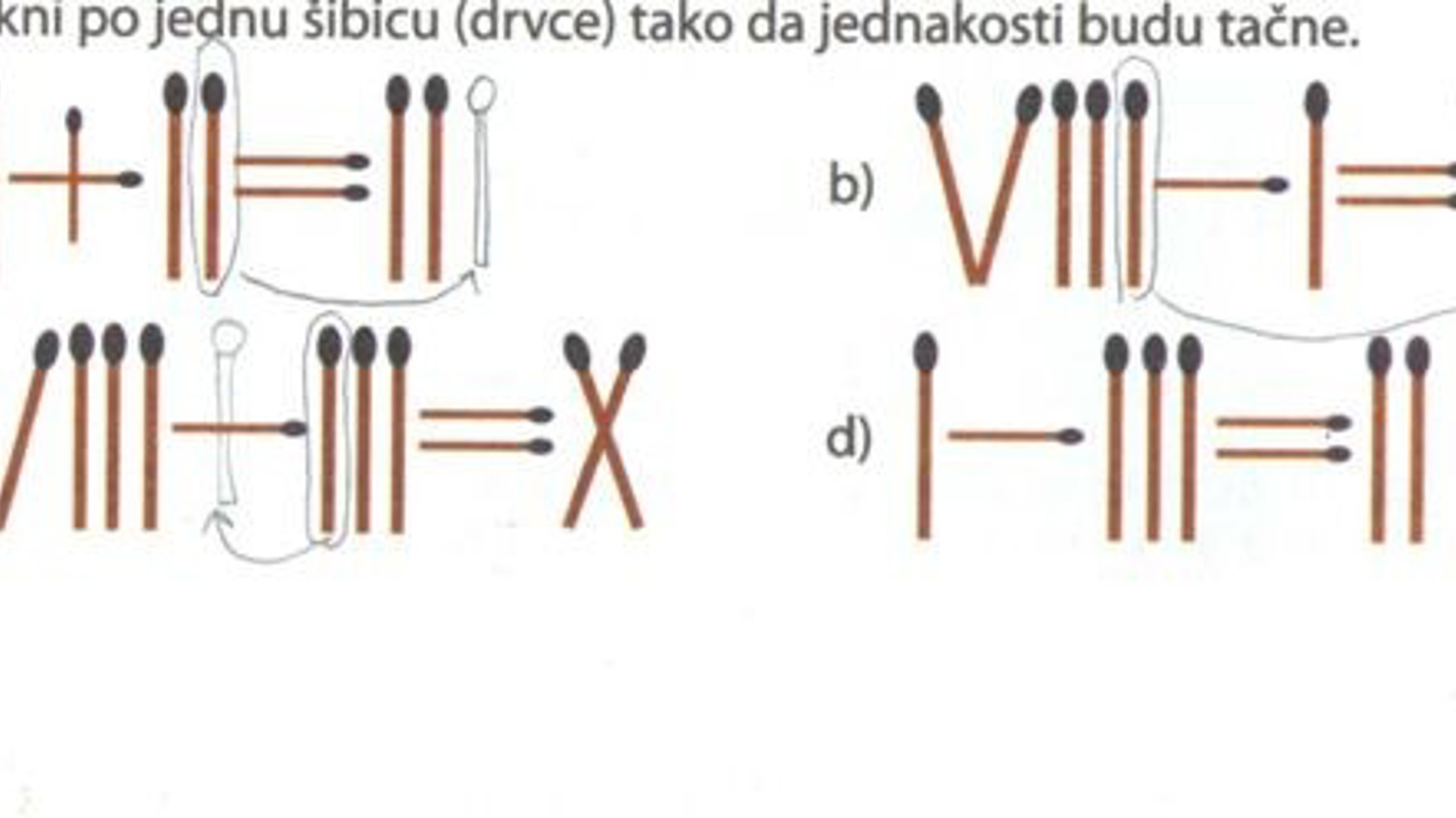
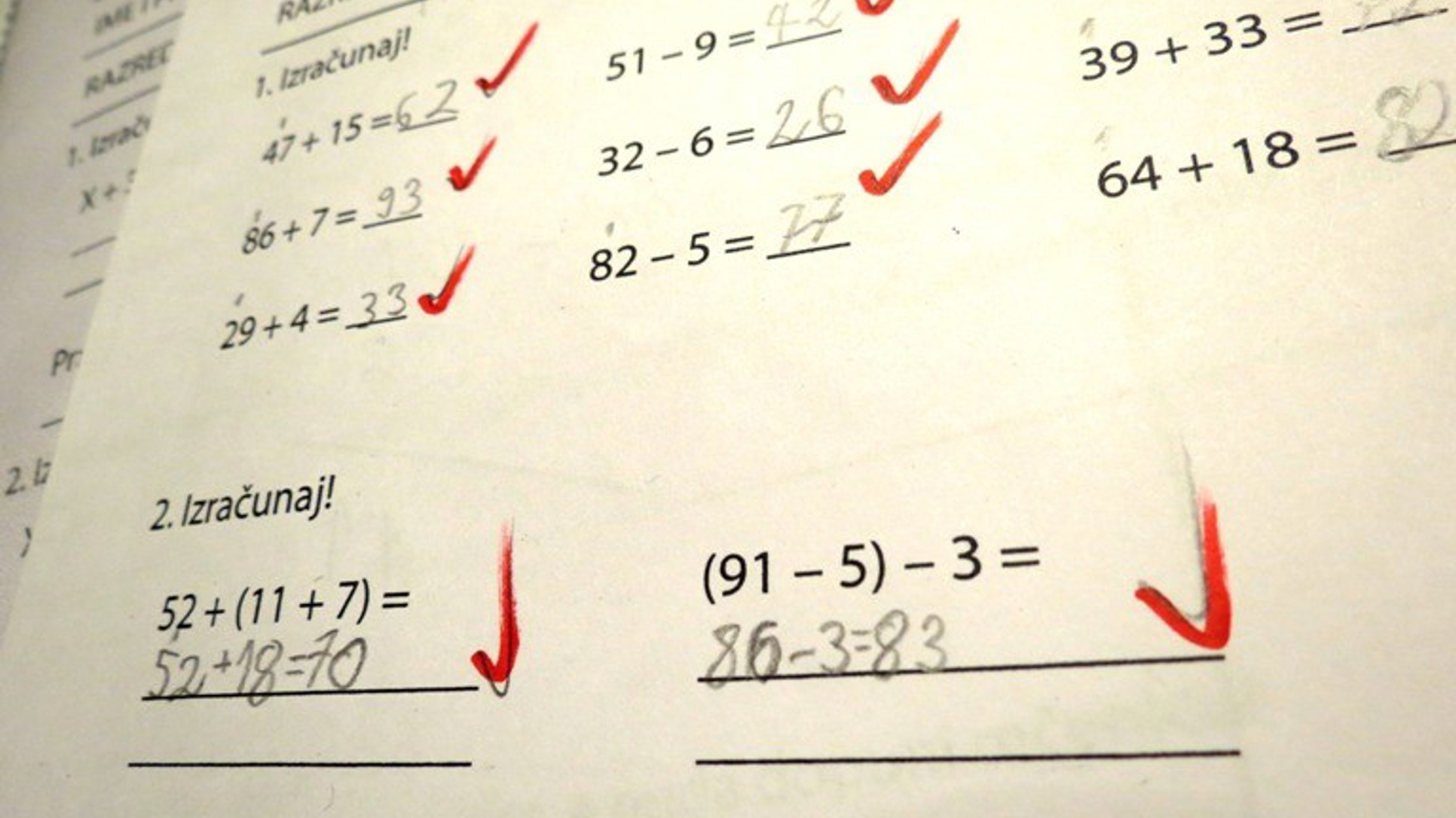Prvo pismo roditelja šestaka: šipak jabuka
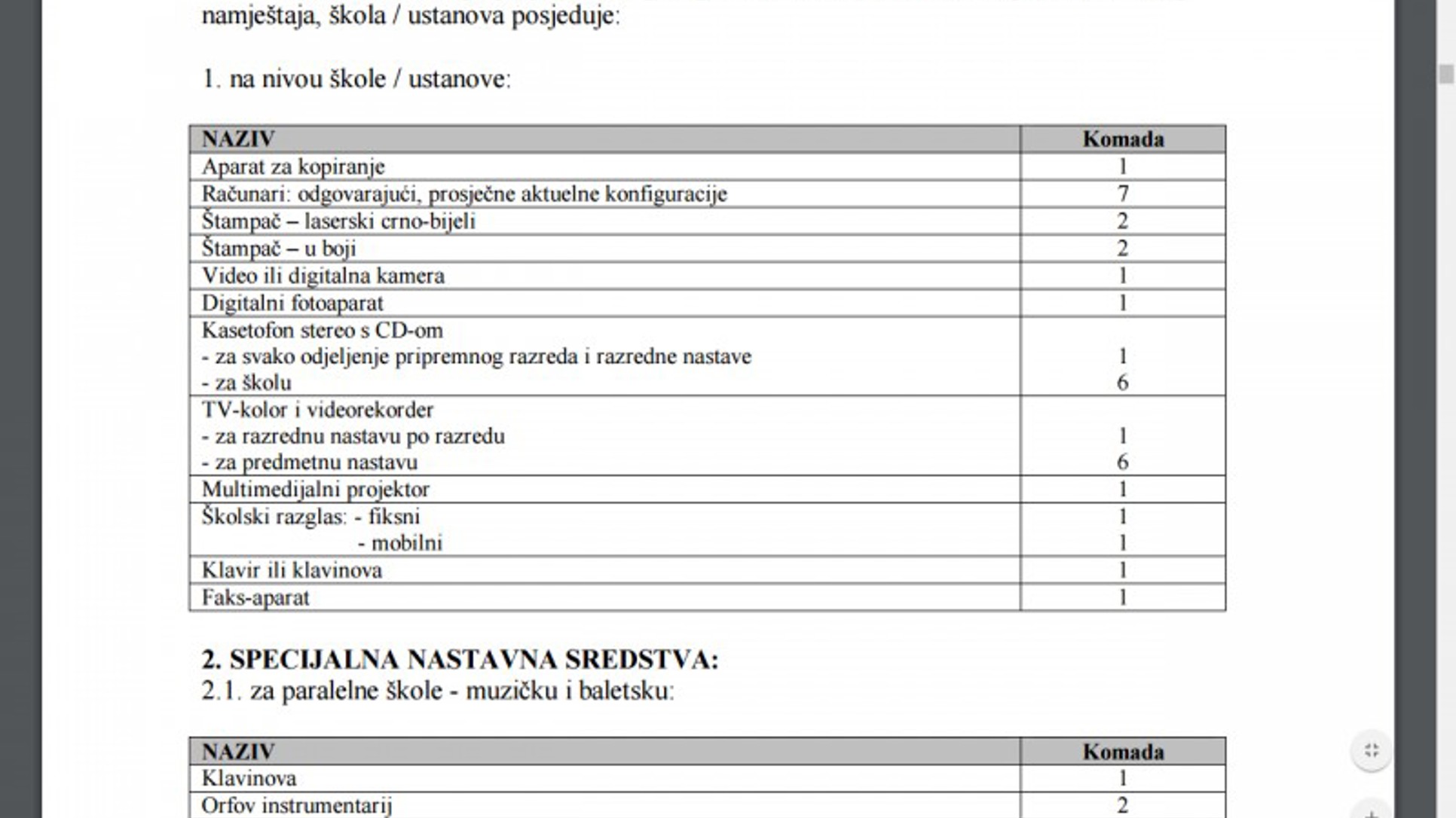
Poštovani prijatelju, šaljem Vam izvod iz udžbenika matematike za VI razred osnovne škole. Matematika je Vaša struka i možda mi pomognete da shvatim kakve veze to ima sa životom. Šta ovdje piše: da ako imamo tri jabuke i podijelimo ih na šestoro djece, svako dijete neće dobiti polovicu, nego šipak. Niko neće dobiti ništa, a svima će ostati tri jabuke. Koja su metodička opravdanja da se matematika radi na ovaj način? Razred je šesti, djeca imaju 11 godina...
Prvi odgovor profesora matematike: Algoritam dijeljenja
Ključna stvar u primjeru koji je povod za ovaj razgovor jest tzv. algoritam dijeljenja. Općenito formulirano u skupu No imamo sljedeću tvrdnju: Ako a∈No, b∈N, tada postoje jedinstveni brojevi q, r∈No, takvi da je a=bq+r, gdje je r<b. Ovdje a zovemo dijeljenikom, b djeliteljem, q količnikom, r ostatkom. Za učenike viših razreda ne bi trebalo predstavljati veći problem da shvate ovaj algoritam dijeljenja u ovoj njegovoj općoj formulaciji. Međutim, pitanje je mogu li učenici šestog razreda to shvatiti. Moj odgovor je da ne mogu sasvim, jer još nisu u stanju da iz matematike konkretnih objekata (brojeva, geometrijskih likova...) pređu u matematiku apstraktnih objekata.
U matematici se sve i sastoji od teorema iskazanih na način sličan ovome algoritmu dijeljenja, ali bavljenje njima i njihovo razumijevanje je nešto što dolazi nakon što se nauči dobro računati i dobro baratati s konkretnim objektima, npr. brojevima. Za to je potrebno da se općenite tvrdnje, (specijalno algoritam dijeljenja), nekako konkretiziraju kako bi ih učenici usvojili i shvatili u razini konkretnih objekata, specijalno zadanih prirodnih brojeva.
Vježbajući ovaj algoritam kroz određeni broj primjera oni će biti u stanju primijeniti taj algoritam na bilo koje zadane brojeve, a odatle pa do shvaćanja algoritma u njegovoj općoj formulaciji još je samo jedan korak. Ukoliko je postojala sumnja da li je u dijelu (b) primjera 2. izveden korektan zaključak, nakon ovih gornjih razmatranja ona bi trebala biti otklonjena.
Međutim, ako bismo pokušali prenijeti ovaj problem u realan život pa postaviti pitanje s jabukama i šestoro djece, odgovor bi bio da će svako dijete dobiti pola jabuke. To je točno, ali taj zaključak nije izveden na osnovu algoritma dijeljenja. Algoritam dijeljenja ne uvodi prave razlomke, tj. brojeve koji nisu prirodni, on govori o rastavu dijeljenika preko djelitelja, količnika i ostatka, koji su svi odreda iz skupa No.
Da utvrdimo šta se zapravo želi uraditi, analizirajmo Primjer 2.(b) detaljnije. Ovdje je a=3, b=7. Tražimo prirodan broj q i prirodan broj r<7 takve da je 3=qb+r. Očito je da mora biti q=0 i r=3. Dakle, količnik je 0, a ostatak je 3. Na sličan način urade se svi preostali primjeri i zadaci sa prikazane stranice. Nakon što ih urade, učenici će biti u stanju da shvate kako radi ovaj algoritam. Iako pojava slova za učenike tog uzrasta može djelovati zbunjujuće, držim da su ovdje učenici na prirodan i metodičan način uvedeni u temu, jer se kroz izradu konkretnih primjera mogu riješiti te zbunjenosti i time se polako, korak po korak, kroz lekcije obrađene na sličan način, uvoditi u ono što zapravo jest matematika, u područje njezine apstraktnosti i općosti. Samo što je put do toga dugačak nekoliko godina.
Drugo pismo roditelja šestaka: Traumatematika
Dragi prijatelju, hvala ti za brz odgovor, iako njime nisam sasvim zadovoljan. Naime, ne vidim zašto bi djetetu koje nikad neće upisati matematički fakultet bilo važno da zna algoritam dijeljenja? Ti, izgleda mi, braniš ovaj pristup iz pozicije matematičara, kome je lojalnost struci na prvom mjestu. Međutim, velikom broju djece je matematika trauma... Nemoguće da su sva ona glupa, lijena, nesposobna... I da se zaista ne može bez tih silnih instruktora, suza, panike, batina, popravnih, jedinica... Vjeruješ li, zaista, da metodičari matematike znaju šta i zašto rade?
Drugi odgovor profesora matematike: Popustljiva nedopustljivost
U sadašnjim okolnostima, nastavni plan i program iz matematike ne treba mijenjati, zato što on ionako predstavlja minimum znanja koji trebaju usvojiti svi budući studenti prirodno-matematičkih, informatičkih i tehničkih znanosti, i ostali koji će na bilo koji način biti vezani za matematiku. Naravno, i radi općeg obrazovanja. Ali je u postojećim okolnostima potrebno promijeniti pristup, tj. način izlaganja toga gradiva, i način ocjenjivanja, imajući senzibiliteta prema učenicima koji ne pokazuju interes za matematiku. Ne može se dopustiti da oni doživljavaju traume zbog neznanja matematike, ali se ne može dopustiti ni da oni koji su sposobni za matematiku nemaju priliku to slušati i učiti na potrebnom nivou. Najbolje bi, svakako, bilo da se promijene ove postojeće okolnosti.
Treće pismo roditelja šestaka: Algoritam okolnosti
Dragi prijatelju, priznajem da me veseli ova naša prepiska, i zahvalan sam na tvom strpljenju. Možda na kraju dođemo do neke jednačine u kojoj jabuke neće trunuti pored gladne djece. Na šta tačno misliš kad kažeš postojeće okolnosti? Kako bi ti uredio nastavu matematike u osnovnoj školi?
I treći odgovor profesora matematike: Ocjene na procjenu
Sadašnje okolnosti su takve da je svaka maštovitost ograničena. Ali, mogli bismo ipak ponovno razmisliti o tome šta koja ocjena treba da znači. Po jednom (starijem) didaktičkom pravilu, da ga interpretiram slobodnije, dvojka treba da predstavlja mogućnost prisjećanja, dakle nju dobiva onaj učenik koji otprilike zna očem se tu radi ali ne više od toga. Tako nitko tko bi se imalo potrudio i pratio nastavu ne bi mogao imati jedan iz bilo kojeg predmeta, pa tako ni iz matematike. Trojka označava sposobnost prepoznavanja sadržaja i njihove kontekstualizacije, četvorka sposobnost reprodukcije sadržaja, a petica se daje za kreativnost, dakle za one koji znaju razmišljati o naučenim sadržajima i na osnovu njih dolaziti do novih, samostalnih, zaključaka. Tako bi bilo mnogo manje petica u našim školama, što je dobro, ali bi bilo i mnogo manje jedinica, jer se za dvojku ne bi tražilo ono što treba da se traži za trojku ili četvorku. Samo da je uvjeriti nastavnike da se drže toga.
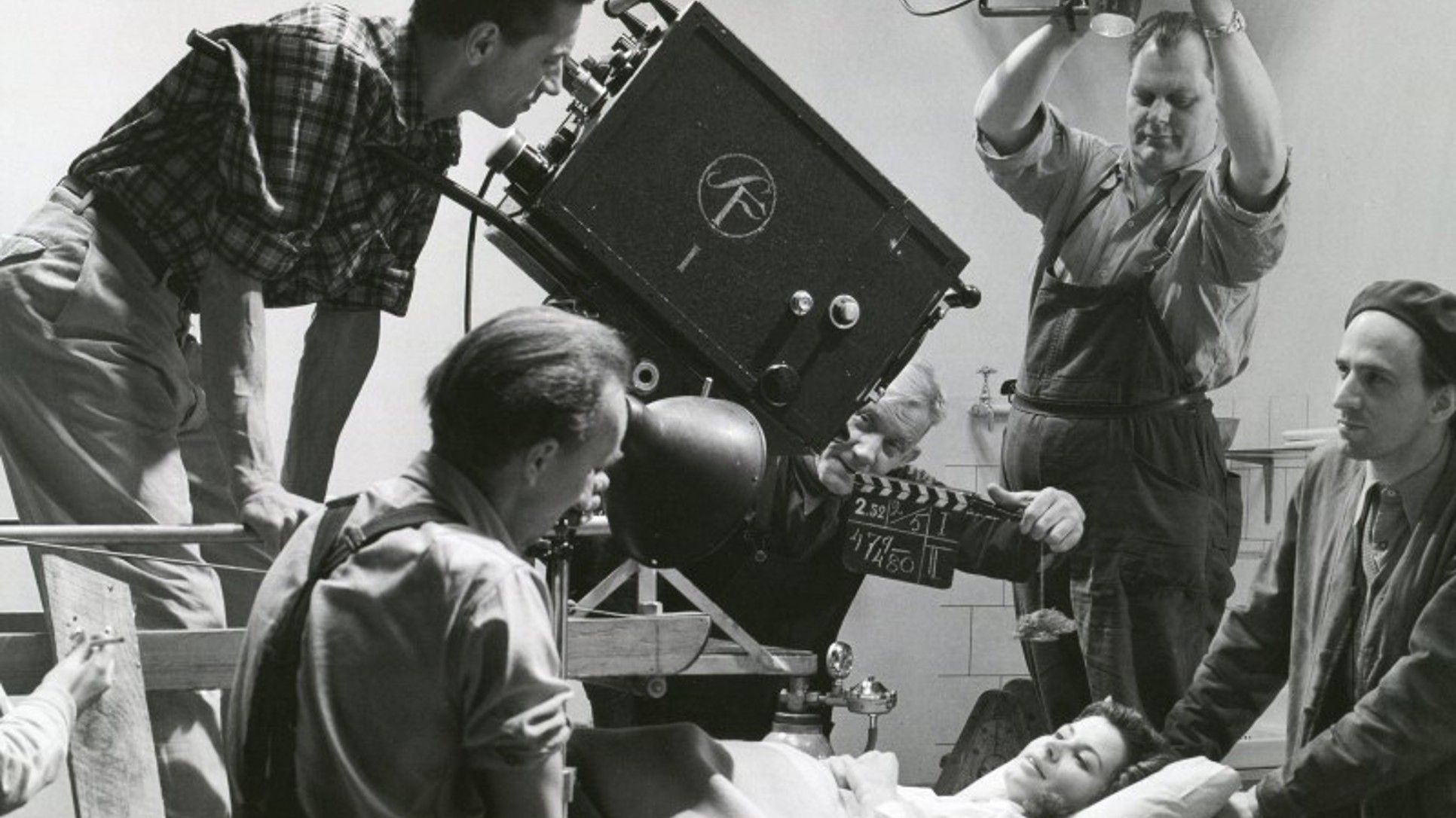
Foto: E. Kurtović