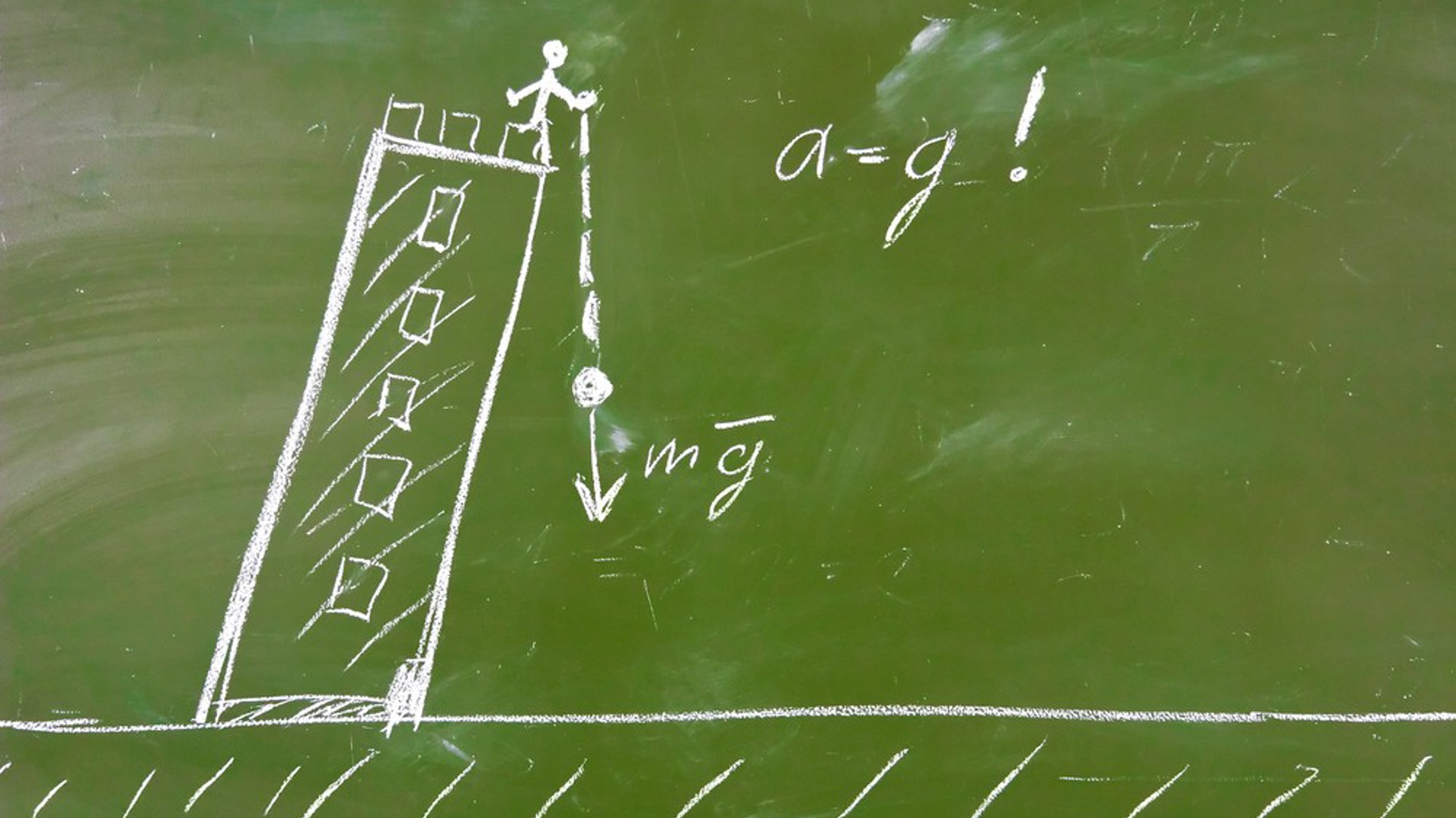
Prije nekoliko godina učestvovala sam na seminaru UWC-IB Inicijative u BiH, koji organizuje Centar za profesionalni razvoj profesora. Cilj seminara bio je predstavljanje savremenih metoda nastave koje se upotrebljavaju u Programu međunarodne mature i mogu se prenijeti u bosanskohercegovačke programe. Tu se pokazalo da nastavnicima trebaju različiti materijali – od priprema za nastavu do primjera eksperimenata, testova, radnih materijala za đake, pa su oni koji su učestvovali na seminarima iz hemije, biologije i fizike pripremili priručnik Primjeri dobre prakse.
Jedan od takvih primjera je simulacija radioaktivnog raspada koju sam provela s đacima. U četvrtom razredu gimnazije imaju pet časova nuklearne fizike. U tih pet časova željela sam dosta toga da kažem, ali sam zaključila da ću im korištenjem ogleda na najbolji način približiti nuklearnu fiziku, odnosno objasniti radioaktivni raspad. Cilj ove simulacije bio je da učenici shvate koncepte slučajne veličine, eksponencijalnu zavisnost (N/N0) nakon vremena (t), gdje je N broj neraspadnutih jezgara, a N0 početni broj jezgri, i na koji način se neki izotop raspada.
Da bi izveli simulaciju radioaktivnog raspada rekla sam im da donesu po par kockica za društvenu igru jamb. Skupili su 45 kockica.
Radioaktivni raspad je slučajan proces, sličan bacanju kockica. Bacanje kockica za jamb i radioaktivni raspad pokoravaju se istim zakonima slučajnih događaja. Svaka kockica predstavlja jedno radioaktivno jezgro nekog izotopa.
Na času smo uzeli kartonsku kutiju, smjestili u nju kockice.
Prvi zadatak bio je da đaci odrede aktivnost uzorka, odnosno broj raspadnutih jezgri radioaktivnog izotopa, koji su označili sa A u jedinici vremena. Odredili su da se izotop raspao ako se kockica pri mućkanju okrene na broj pet. Promućkali su kutiju i iz nje izvadili samo kockice na kojima je bio okrenut broj pet. Zabilježili su taj broj kockica u tabeli kao broj raspadnutih jezgri. Upisali su i broj kockica koje su ostale u kutiji. To je broj neraspadnutih jezgri. Postupak su ponavljali sve dok ima jezgri (kockica), ili bar deset puta. Svaki put su u tabeli izračunali odnos N/N0.
Tabela 1. Izotop A
|
Broj bacanja |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Broj raspadnutih jezgri |
13 |
7 |
5 |
6 |
3 |
4 |
2 |
1 |
2 |
1 |
|
Broj jezgri koji je ostao (N) |
32 |
25 |
20 |
14 |
11 |
7 |
5 |
4 |
2 |
1 |
|
N/N0 |
2,46 |
3,57 |
4,0 |
2,33 |
3,66 |
1,75 |
2,5 |
4 |
1 |
1 |
Drugi zadatak bio je da grafički predstave rezultate iz tabele. Zadala sam im da sami kod kuće nacrtaju grafik, jer nisu imali vremena za jedan čas. Na X osu trebali su unijeti vrijednosti koje predstavljaju redni broj bacanja, a na Y osu odnos broja preostalih kockica i ukupnog broja kockica, dakle N/N0. Kroz unesene tačke trebalo je provući glatku krivu, tako da dobiju eksponencijalnu zavisnost ovih veličina.
Đaci su izvođenjem ove simulacije uz igru odredili aktivnost uzorka, odnosno broj raspadnutih jezgri nekog radioaktivnog izotopa u jedinici vremena. Na kraju su rekli da je čas bio jako zanimljiv. Svidjelo im se to što sami rade i istražuju. Uspješno su dolazili do zaključaka i bili su dosta ponosni na sebe kada bih ih pohvalila za odrađeno. Pošto sam radila s učenicama i učenicima četvrtog razreda, kojima predajem već četvrtu godinu i koji su navikli na interaktivni način rada, lako su sarađivali. Problem se stvara kada ne znaju za takav način rada i kada moram dati sve od sebe da ih animiram.
Nadam se da će s godinama nastavnice i nastavnici u svim školama interaktivno predavati fiziku, jer će to biti od velike koristi kako učenicima, tako i njima samima. Apstraktni pojmovi, kao što su radioaktivnost, radioaktivno zračenje, radioaktivni raspad, đacima su često potpuno nepoznati. U nedostatku predznanja, djeca veoma teško usvajaju nove sadržaje. Istovremeno, u udžbenicima su nastavne jedinice o nuklearnoj fizici napisane i ilustrovane sa stanovišta stručnjaka. Puno je matematičkih formula i definicija. Djeca se trude da to nauče napamet i izrecituju. Udžbenik treba da sadrži više atraktivnih i interdisciplinarnih sadržaja, više kreativnih izazova, simulacija za razmišljanje i ogleda. Poželjno je da u njemu postoje slike i ilustracije vezane za nastavnu jedinicu, jer one zadržavaju pažnju.
Manjak časova u III i IV razredu gimnazije veliki je problem, jer za to vrijeme nastavnice moraju objasniti jedinicu, izvesti ogled, uraditi zadatke, testirati đake. Zato se trudim da učenike nagovorim da sami istražuju, uvjerim ih da su sposobni za samostalno učenje i permanentno obrazovanje. Oni trebaju istraživati, razvijati svoje kreativne sposobnosti, tragati za odgovorima na postavljena pitanja ili zadate probleme, analizirati, zaključivati, obrazlagati rezultate saznanja. Kao nastavnica, naučila sam da se ne trebam strogo držati pripreme koju uradim za čas ukoliko dječiji odgovori i pitanja vode raspravu u drugačijem smjeru. Često im govorim da istražuju u prirodi, izvode oglede, demonstriraju, koriste simulacije i na računaru, jer tako stiču znanja sopstvenom aktivnošću.