Kao srednjoškolska profesorica fizike u Unsko-sanskom kantonu osjećam potrebu da se osvrnem na udžbenik fizike za drugi razred gimnazije koji su potpisali Hrustem Smailhodžić, Smajo Sulejmanović i Vladimir Paar, i koji datira iz davne 2003. godine (do 2022. djeca su imala jedino taj izbor naših izdavača, pisan na hrvatskom jeziku). Naime, sve vrijeme imam dojam da su bh. autori dijelove udžbenika koje je pisao Paar u Hrvatskoj naprosto kopirali, umjesto da ponešto detaljnije objasne i učine da udžbenik bude razumljiviji.
Prvo poglavlje je Molekularno-kinetička teorija plinova i autori su kratko definisali molekul, njegove dimenzije, nabrojali osobine idealnog plina (gasa), pa su prešli na realan gas i odjednom uveli pojmove pritisak, temperatura, i nabrojali pojmove za plinske zakone. U donjem desnom uglu stranice nacrtana je kocka sa mnogo tačkica, ispod koje ne piše ništa jer su autori smatrali da je dovoljno što u tekstu piše da je to model idealnog plina.
Na ovu sliku uputila me učenica drugog razreda koja je željela da joj pojasnim crtež. Da bih joj objasnila o čemu se radi izvela sam đake ispred table, njih 20, i rekla da se pokušaju kretati u tom prostoru. Nastala je živa zbrka, guranje smijanje... Rekla sam im da su sada oni realan gas, da je mnogo sudara među njima i sa zidom učionice. Onda sam ih odvela u fiskulturnu salu i rekla da se tu kreću slobodno i da su onda idealan gas, jer je manje međusobnih sudara.
Kako bi izgledala ova stranica udžbenika da sam je ja pisala?
Vjerovatno bih krenula od koncepta temperature, o kojoj autori kasnije pišu da je temperatura povezana sa našim osjetom toplo hladno, a mjeri se termometrom, i navode samo živin termometar!?
Kad je riječ o termometrima, i ovdje se propustila važna informacija. Mogao se spomenuti i pirometar i podatak da je najraniji, Hindley pirometar, koji datira iz 1752. godine, postavljen u Londonskom muzeju nauke i proizveden za Kraljevsku kolekciju.
Naučna definicija temperature manje je dvosmislena nego naša osjetila za vruće i hladno, kako to pišu autori. Temperatura je definisana kao ono što mi mjerimo termometrom, dakle kao stepen zagrijanosti tijela, iako ćemo kasnije vidjeti koliko je temperatura povezana s kinetičkom energijom atoma i molekula... Ovaj koncept je doista evoluirao od običnog, svakodnevnog iskustva ljudske percepcije na vruće i hladno. No, šta ovo za djecu znači i u kakve zablude je može odvesti?
Tu bih postavila nekoliko praktičnih ogleda, sa fotografijama i opisom. Naprimjer: ako stavite jednu ruku u posudu s toplom vodom, a drugu u posudu s hladnom vodom, a zatim obje ruke stavite u posudu s mlakom vodom, mlaka voda će biti hladnija ruci koja je bila u vrućoj vodi, a ugodno topla ruci koja je bila u hladnoj vodi.
Na desnu stranu udžbenika koji je ovdje gotovo prazan postavila bih Upozorenje na zabludu i pitanja: jesu li u zimsko jutro drvo na terasi i metal na biciklu iste temperature; zašto većina ljudi osjeća da je mnogo toplije u vrućim, vlažnim danima nego u vrućim, suhim danima?
U ovom udžbeniku navedene su dvije temperaturne skale i način preračunavanja iz stepena Celzijusa u stepene Kelvina (strana 8 i 9), uz fotografije čiji opis ne postoji ni ispod slike ni u tekstu (slika 1.9. c)). Ovdje bi, recimo, bilo zanimljivo spomenuti ko je bio lord Kelvin i zašto je bio lord, te da li je to njegovo ime. Ali, šta je sa skalom Farenhajt?
U Engleskoj i Sjedinjenim Američkim Državama koristi se Farenhajtova skala, koju je predložio njemački naučnik Daniel Gabriel Fahrenheit 1724. godine.
Sad bi bilo zgodno pokazati im na pametnim telefonima aplikaciju za preračune. Također, trebao bi se naći podatak o najnižoj laboratorijski postignutoj temperaturi u stepenima Kelvina kako bi djeca dobila konceptualna saznanja o uslovima svijeta u blizini postizanja apsolutne nule.
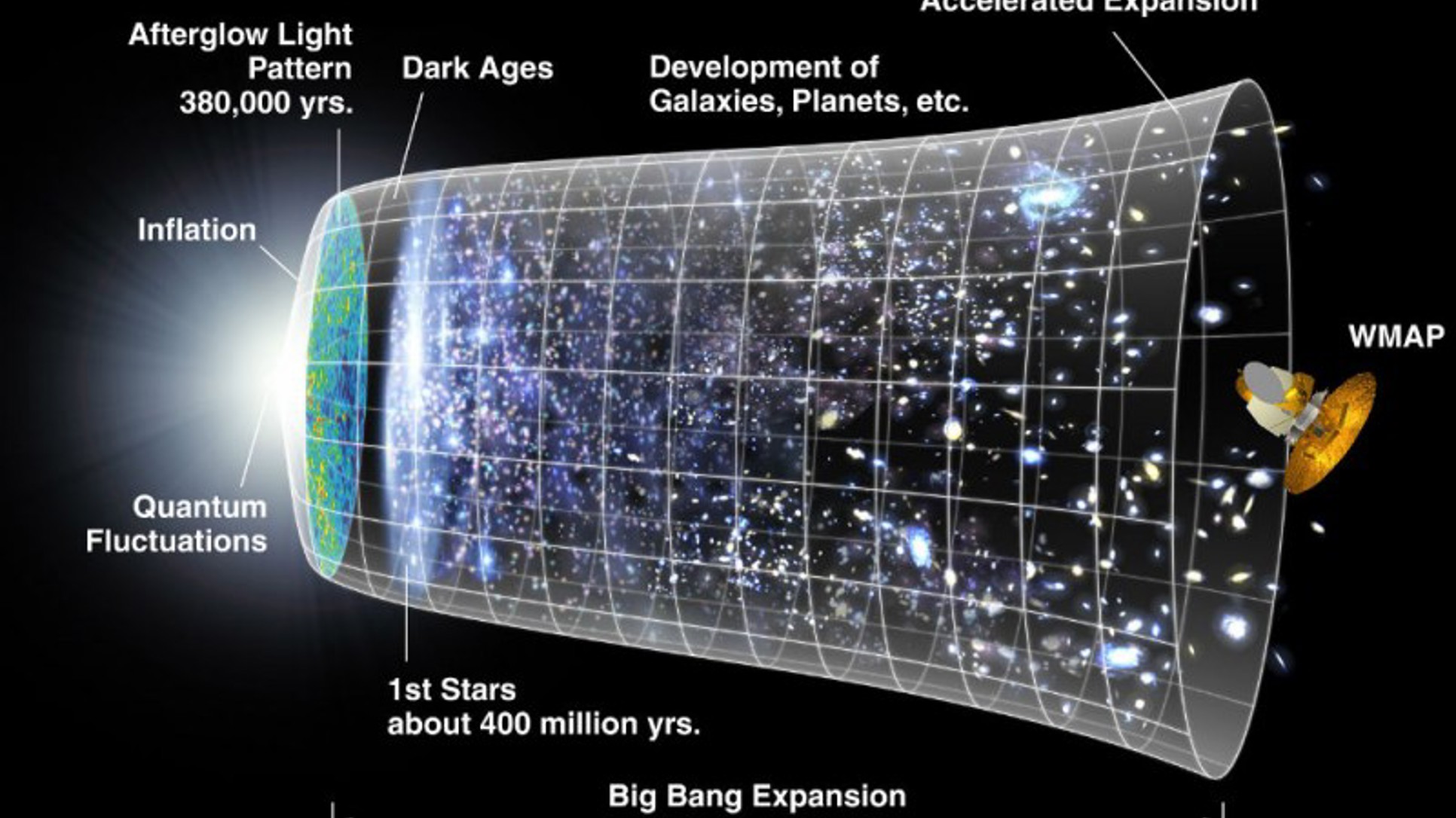
Slika na koju se pozivaju autori opet je famozna kocka u kojoj su kuglice na 0 stepeni Kelvina i stiče se dojam da apsolutno miruju. Ali, zar ne bi bilo dobro da su se osvrnuli na pitanje o dešavanja s tijelima u blizini apsolutne nule? Danas, naprimjer, znamo da Boomerang nebula ima temperaturu jednog Kelvina, a da se u vrijeme (pre)pis(iv)anja udžbenika znalo da se postigla temperatura od 1 pikokelvina (što je 10-12, odnosno 0,000000000001 K), što je također interesantan podatak.
U udžbeniku se pojavljuje i obrazac za srednju kinetičku energiju molekula i konstanta kB, koja ni na jednom mjestu nije objašnjenja (čija je to konstanta i koja je njena uloga u obrascu); samo je s neba pala njena vrijednost! Radi se o Boltzmannovoj konstanti i valjda je Boltzmann zaslužio da se barem jednom rečenicom spomene u ovom kontekstu kao veliki austrijski fizičar, jedan od osnivača molekularno-kinetičke teorije. U njegovim djelima molekularno-kinetička teorija prvi put se pojavila kao logički koherentna, konzistentna fizička teorija. Boltzmann je dao statističku interpretaciju drugog zakona termodinamike. (Borac po prirodi, strastveno je branio potrebu za molekularnom interpretacijom termalnih fenomena i preuzeo na sebe teret borbe protiv naučnika koji su poricali postojanje molekula.)
Bilo bi jako dobro da su autori kreirali rubriku Da li ste znali? Djeca to vole. Tu su mogli navesti broj atoma zraka koje svaki čovjek udahne jednim udisajem – vjerovatnoća je da danas, u 21. vijeku, udahnemo barem 100 miliona atoma koje je disao Leonardo da Vinci! (Naš prijatelj atom, grupa autora, Nauka i škola, 1962)
Ima i jedna slika uz koju je kao objašnjenje za Maxwellove raspodjele po brzinama napisano: Na temelju tog zakona prikazali smo na slici 1.6. raspodjelu molekula kisika prema brzinama pri temperaturi 0°C, a sa slike se vidi, na primjer, da na temperaturi 0°C dvostruko više molekula ima brzinu 300 m/s, nego brzinu 600 m/s. Napominjemo da zakon koji opisuje raspodjelu molekula prema brzinama ne određuje brzinu svake pojedine molekule nego samo udjele molekula koje će se kretati nekom određenom brzinom. Zato kažemo da takav zakon ima statističko obilježje.
Je li se ovdje moglo dati objašnjenje udjela molekula i statističkog obilježja? Je li se trebalo pozabaviti samim oblikom krive koja ima maksimum i asimptotski se približava x-osi (jako blizu je, ali nikad ne dodiruje x-osu); vrlo velike brzine su malo vjerovatne, to je moguće samo pod uslovom da će molekul, u mnogim sudarima s drugim molekulima, primiti energiju, a ne dati je, što je nevjerovatno. Mogla se skrenuti pažnja učenicima da graf nije simetričan – na desnom kraju grafikona većih brzina nalazi se duži rep, a na slici je ova asimetričnost gotovo neprimjetna. Šta je s najvjerovatnijom brzinom? Gdje je ona prikazana na grafiku? Molekuli zraka koji nas okružuju ne putuju istom brzinom, čak i ako je sav zrak na stalnoj i istoj temperaturi. Neki od molekula zraka će se kretati izuzetno brzo, neki će se kretati umjerenom brzinom, a neki će se jedva kretati. Zbog toga ne možemo postavljati pitanja poput: Kolika je brzina svakog molekula zraka u gasu?
Dakle, umjesto pitanja o bilo kojoj određenoj brzini molekula gasa, moglo bi se postaviti pitanje: Kakva je raspodjela brzina u gasu na određenoj temperaturi?
I tako dalje, i tako dalje.
Eto, napisala sam šta treba promijeniti u udžbeniku fizike za 2. razred gimnazije, i sad su na potezu izdavači.
Dobro, dopala mi se kod statističke zakonitosti slika u kojoj se đacima približava pojam vjerovatnog događaja (mačka lovi miša) i manje vjerovatnog događaja (miš lovi mačku).
I, na kraju, realno se zapitam je li baš sav posao i krivnja na izdavačima.
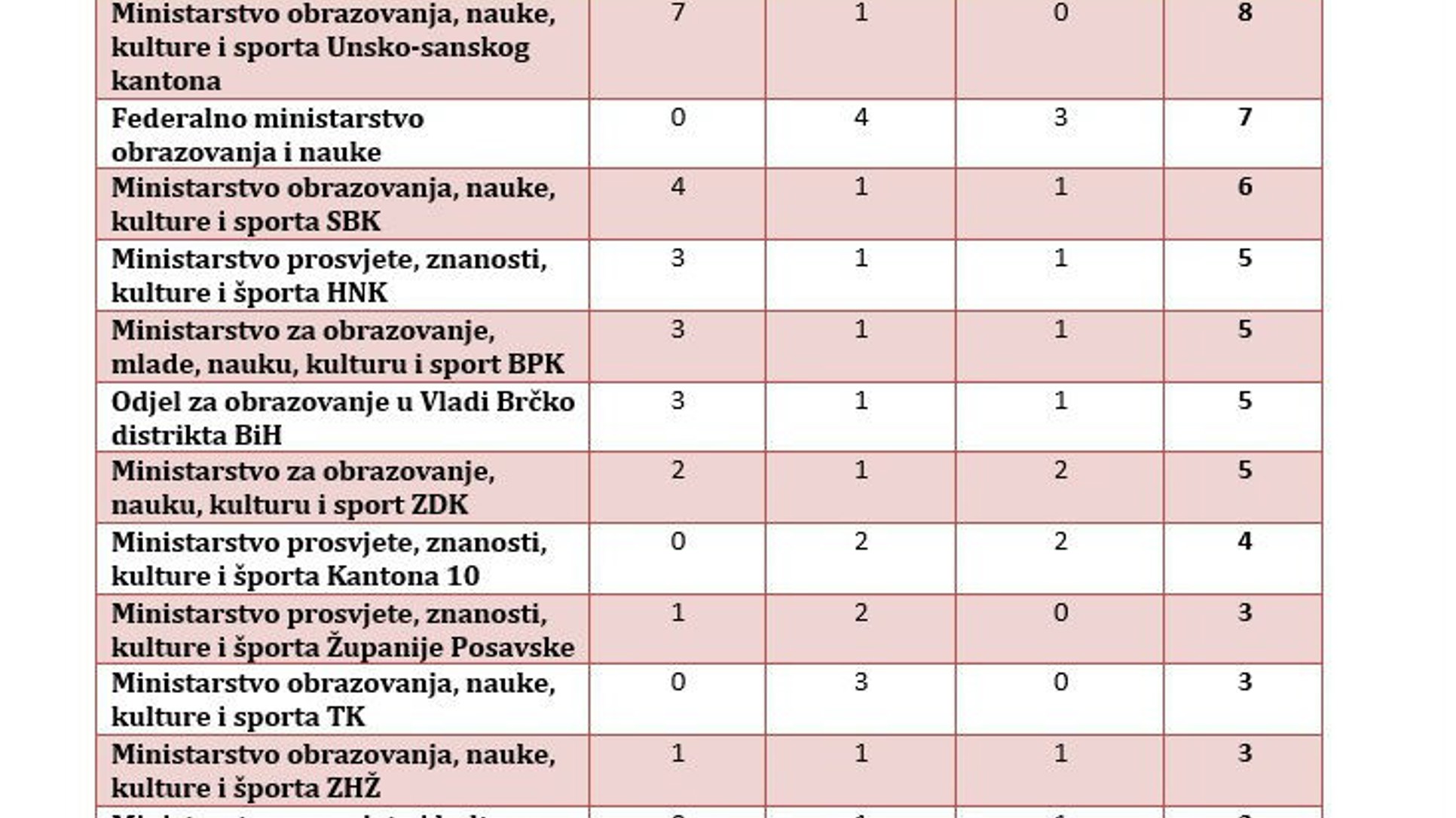
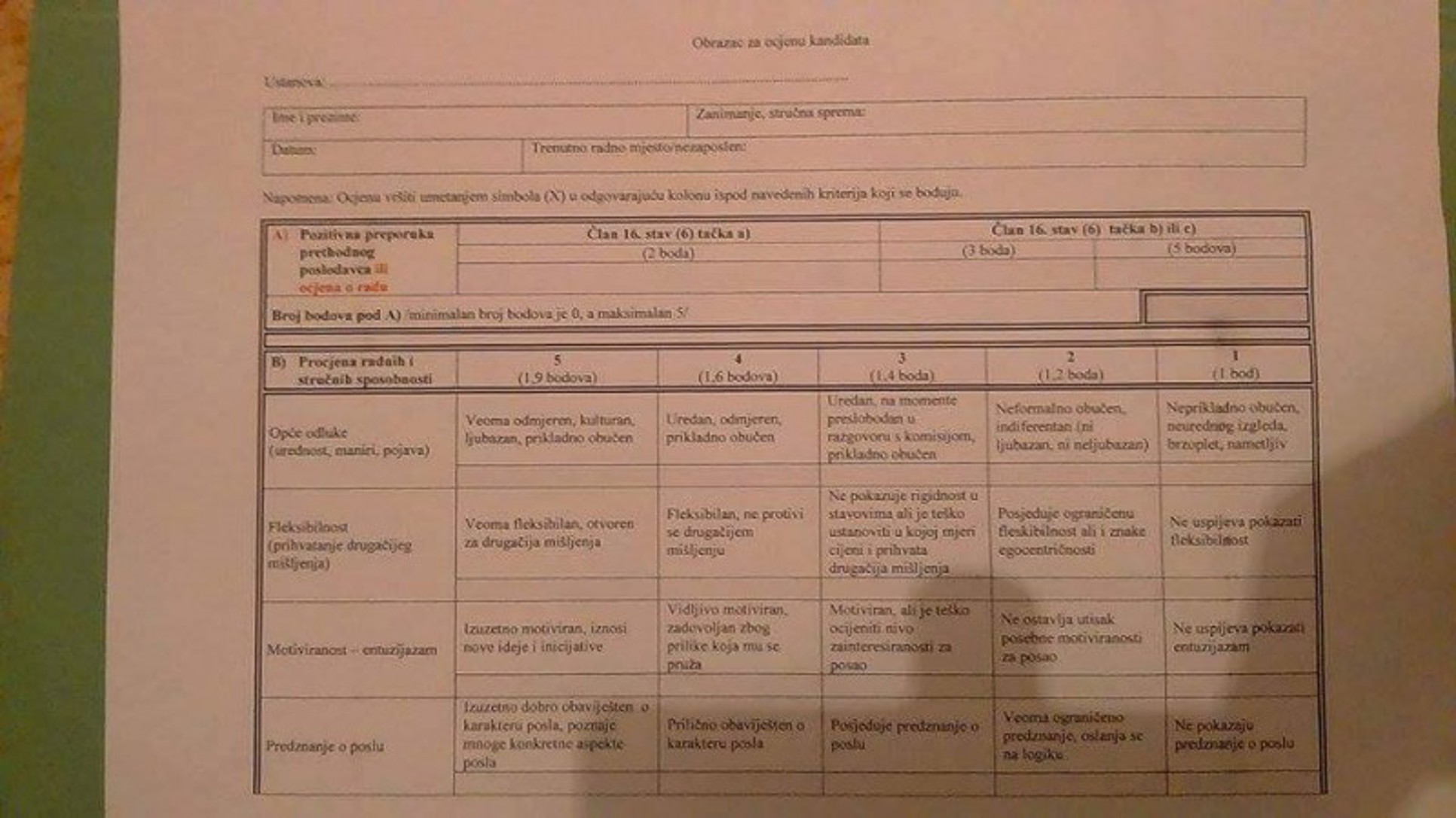
Kolika je odgovornost ministarstva, može li ono tražiti od nastavnika/autora da ponude nove i bolje rukopise? I sami nastavnici bi trebali biti uključeni u izradu kriterija za dobar udžbenik, a taj bi posao trebali voditi stručnjaci s univerziteta, i to predano, a ne formalno.
A jesmo li i mi, nastavnici i stručni aktivi, jednako krivi za ovu situaciju s udžbenicima? Imamo li pravo reći da nećemo raditi po lošem udžbeniku? Kakve bismo posljedice tako lošeg ponašanja imali?