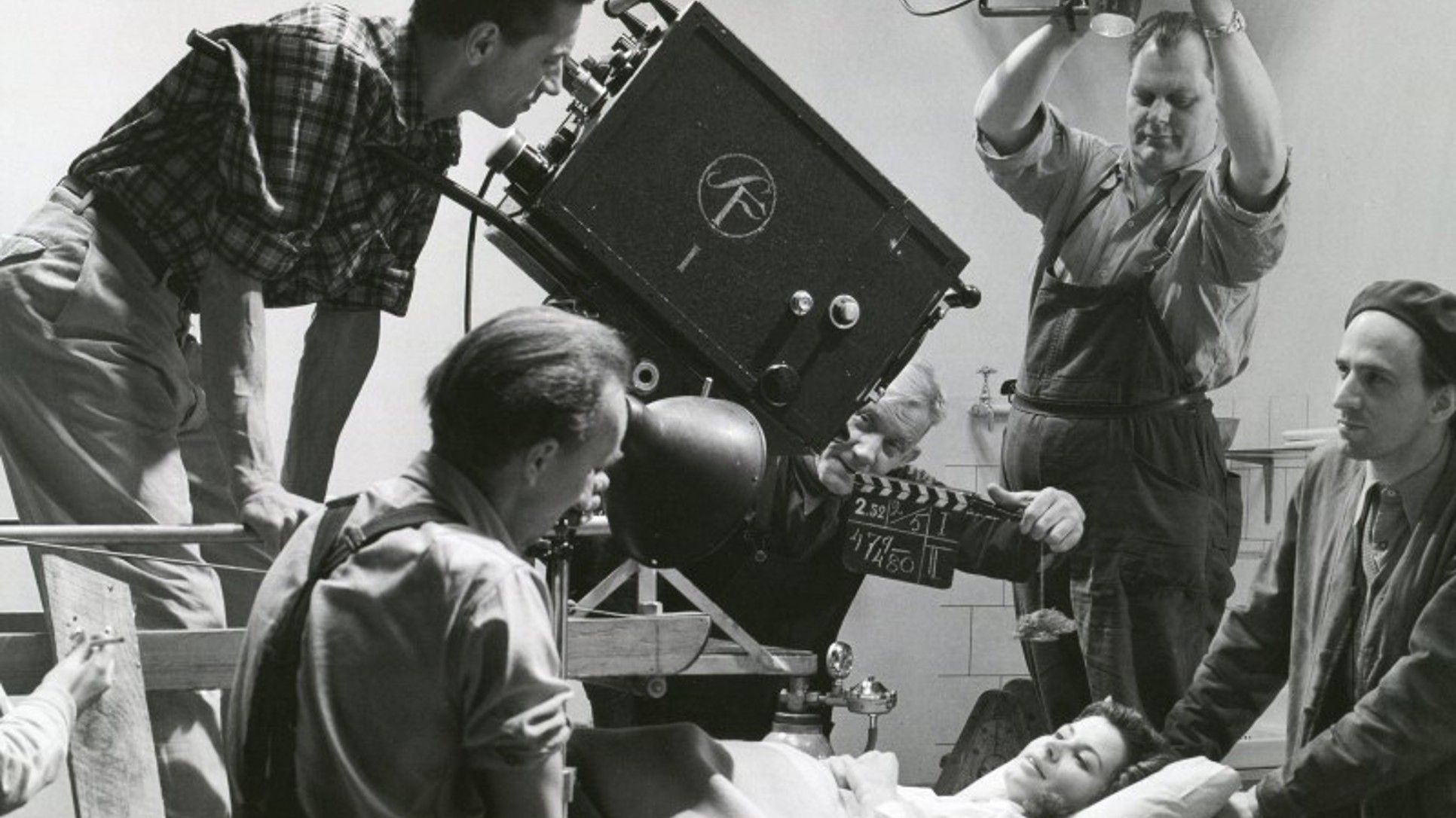
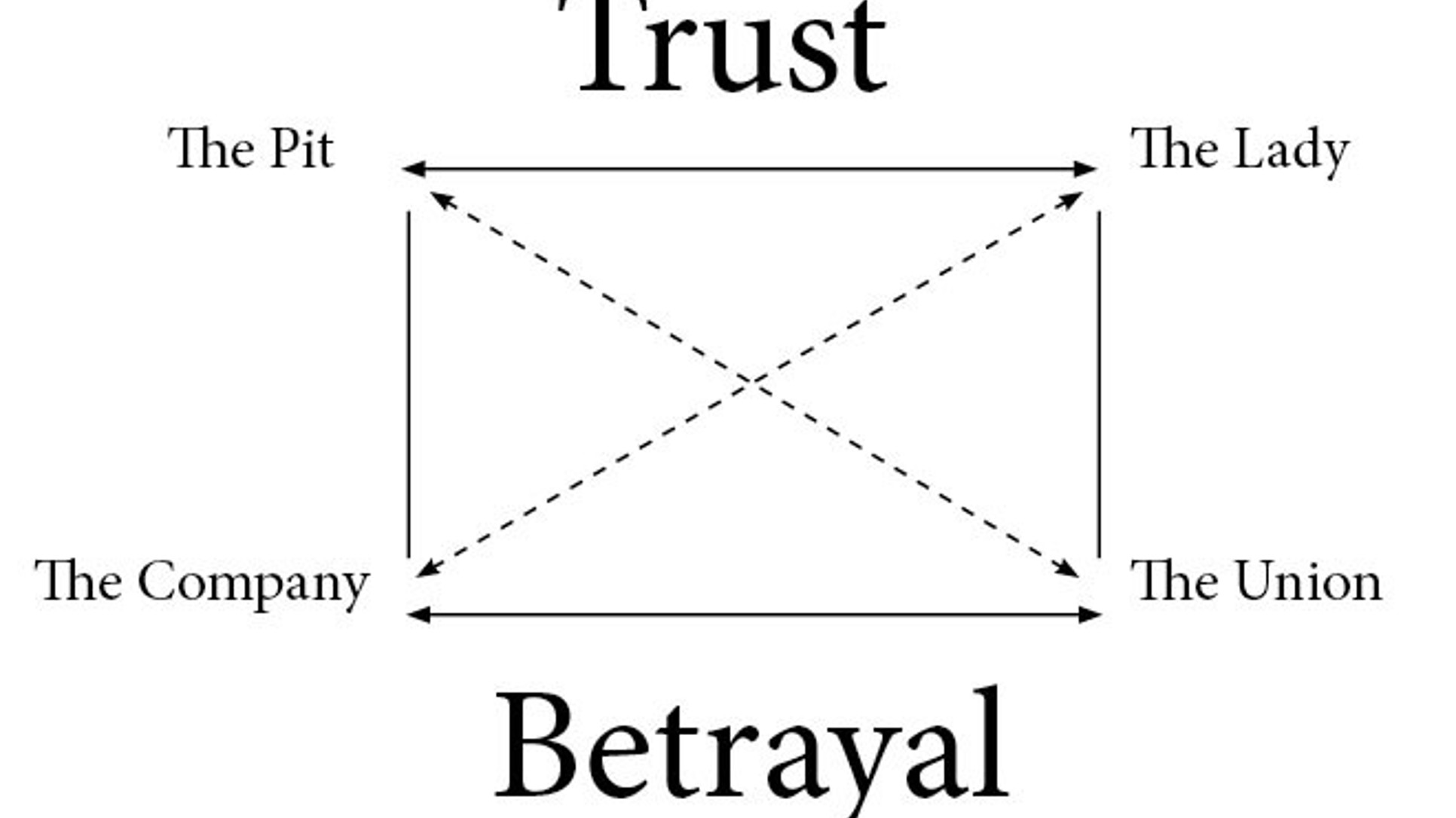
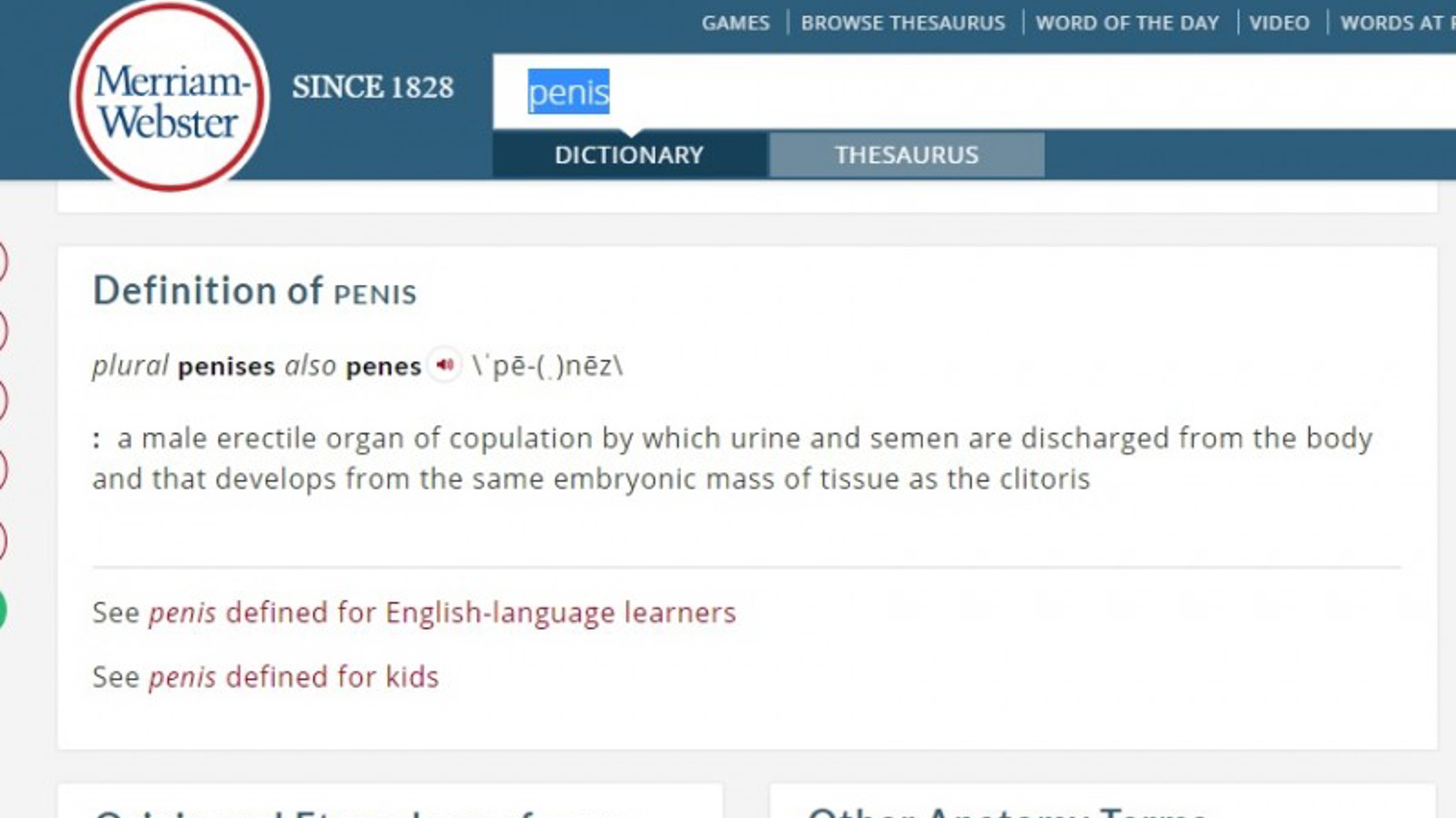
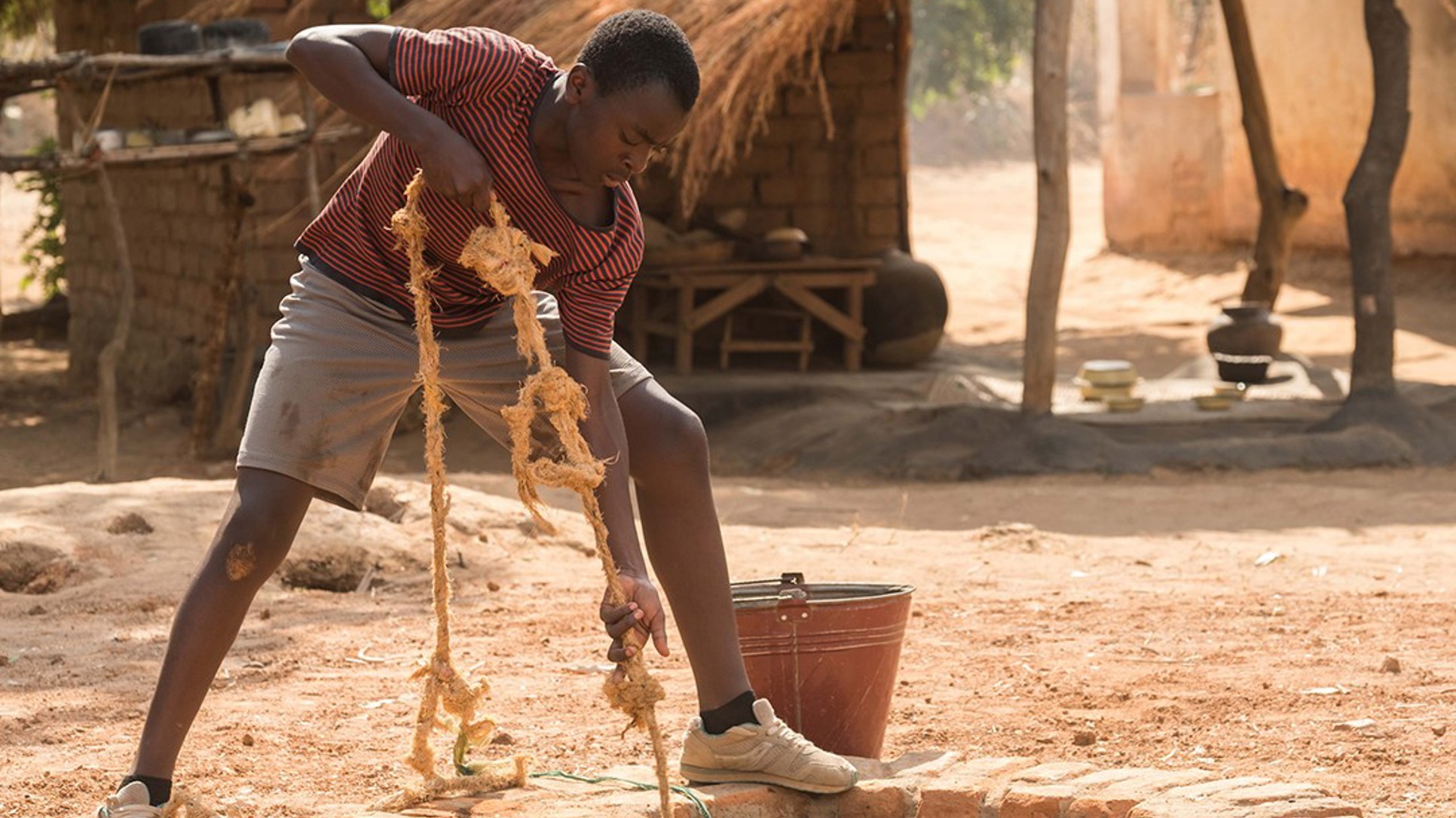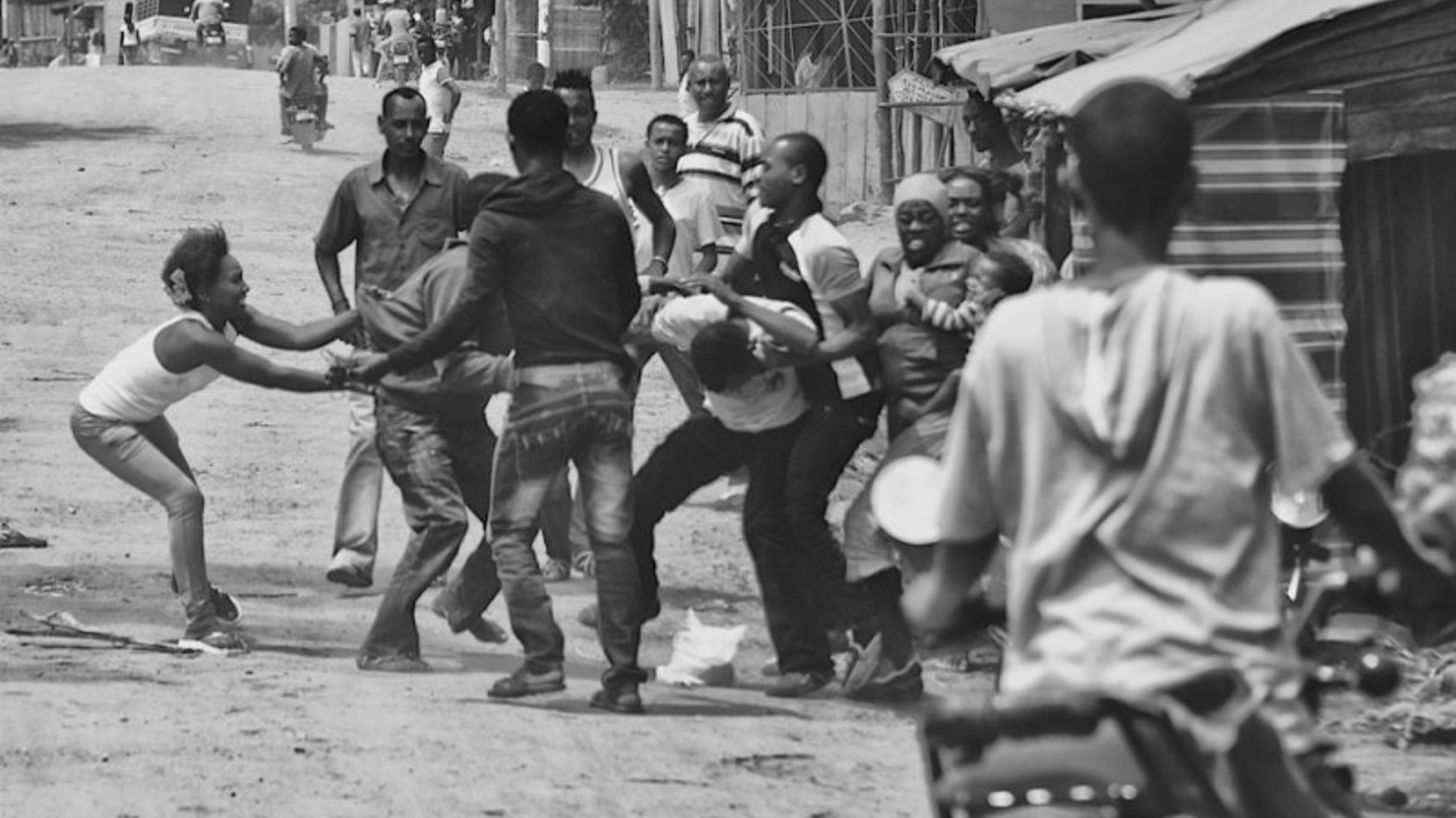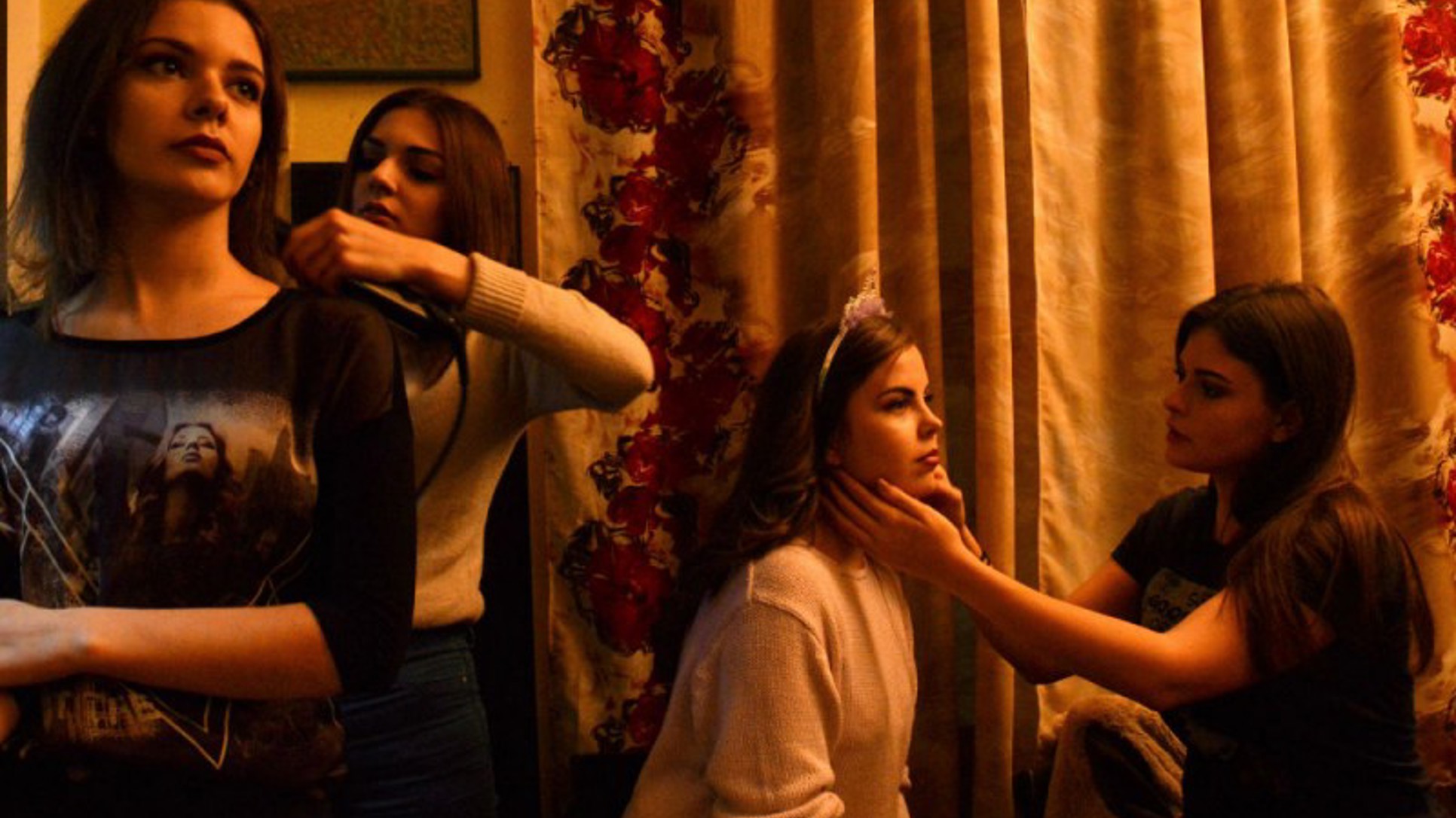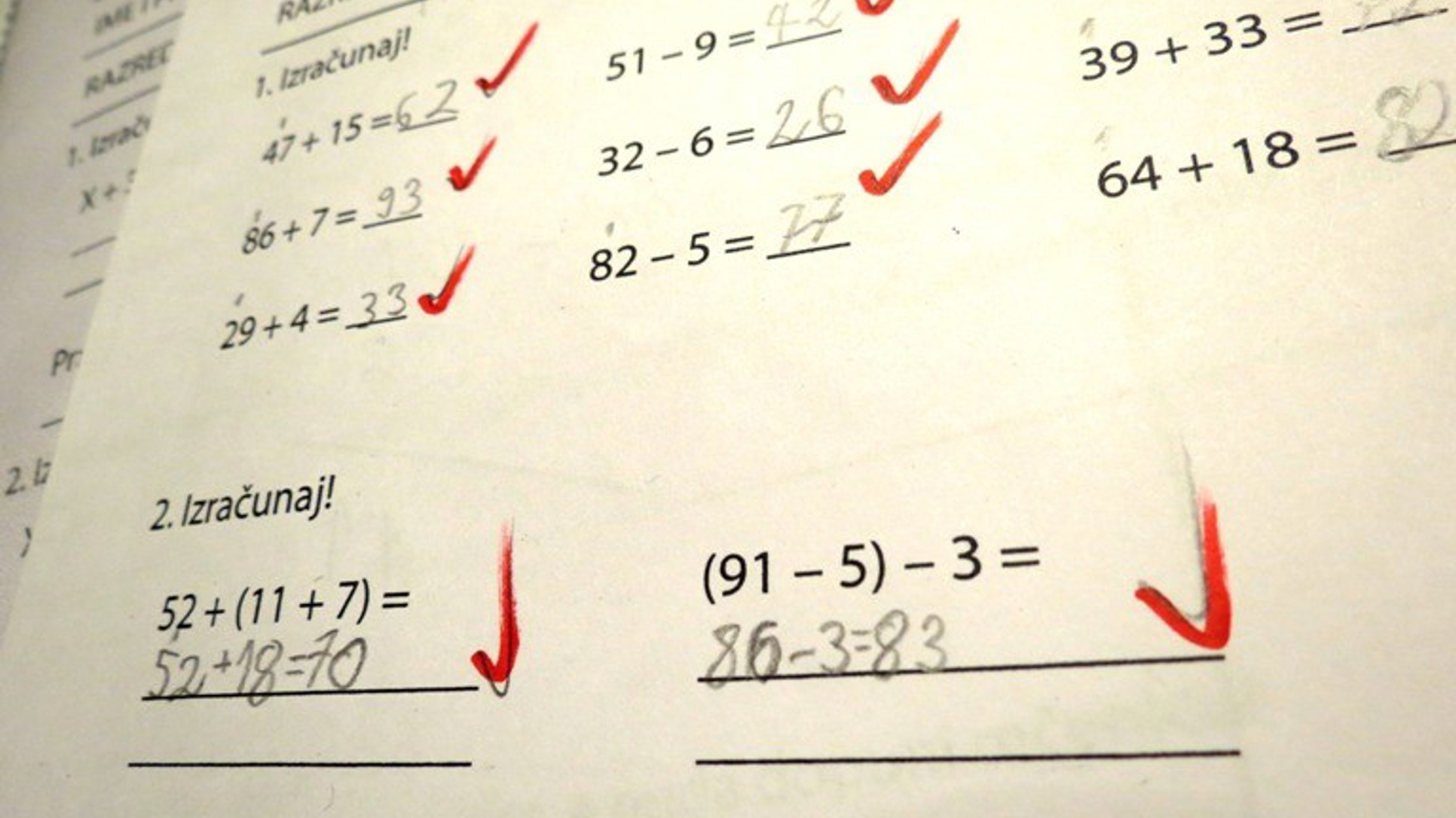Čemu je, nakon pojednostavljenja, jednak izraz x4·(-x2):x5?
Zaokruži slovo ispred tačnog odgovora.
- x5
- -x5
- x15
- -x15
Odredi vrijednost parametra b u jednačini y=-2x+b, ako je nula funkcije 3.
Zaokruži slovo ispred tačnog odgovora.
- b = 0
- b = 3
- b = 6
- b = -6
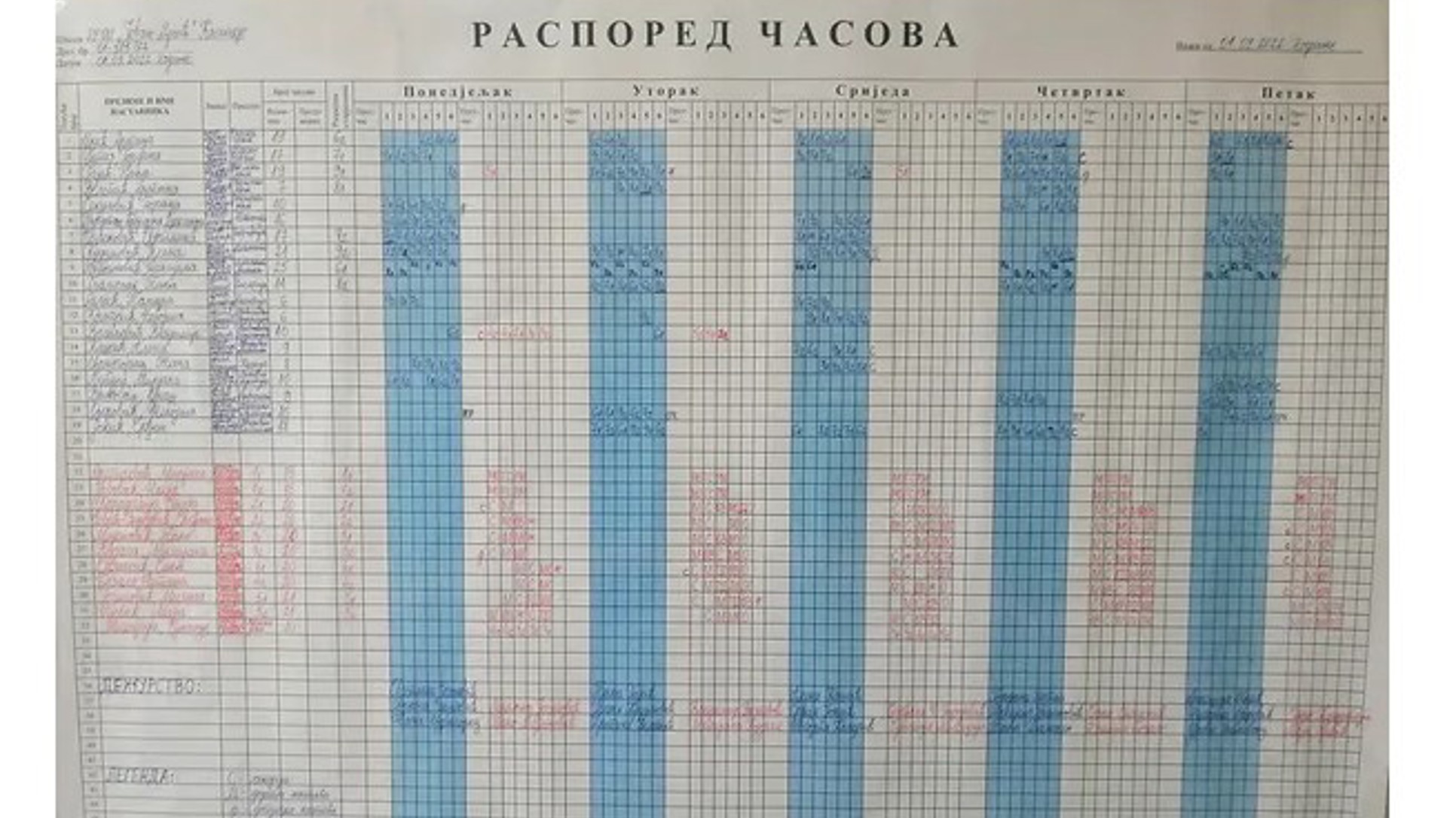
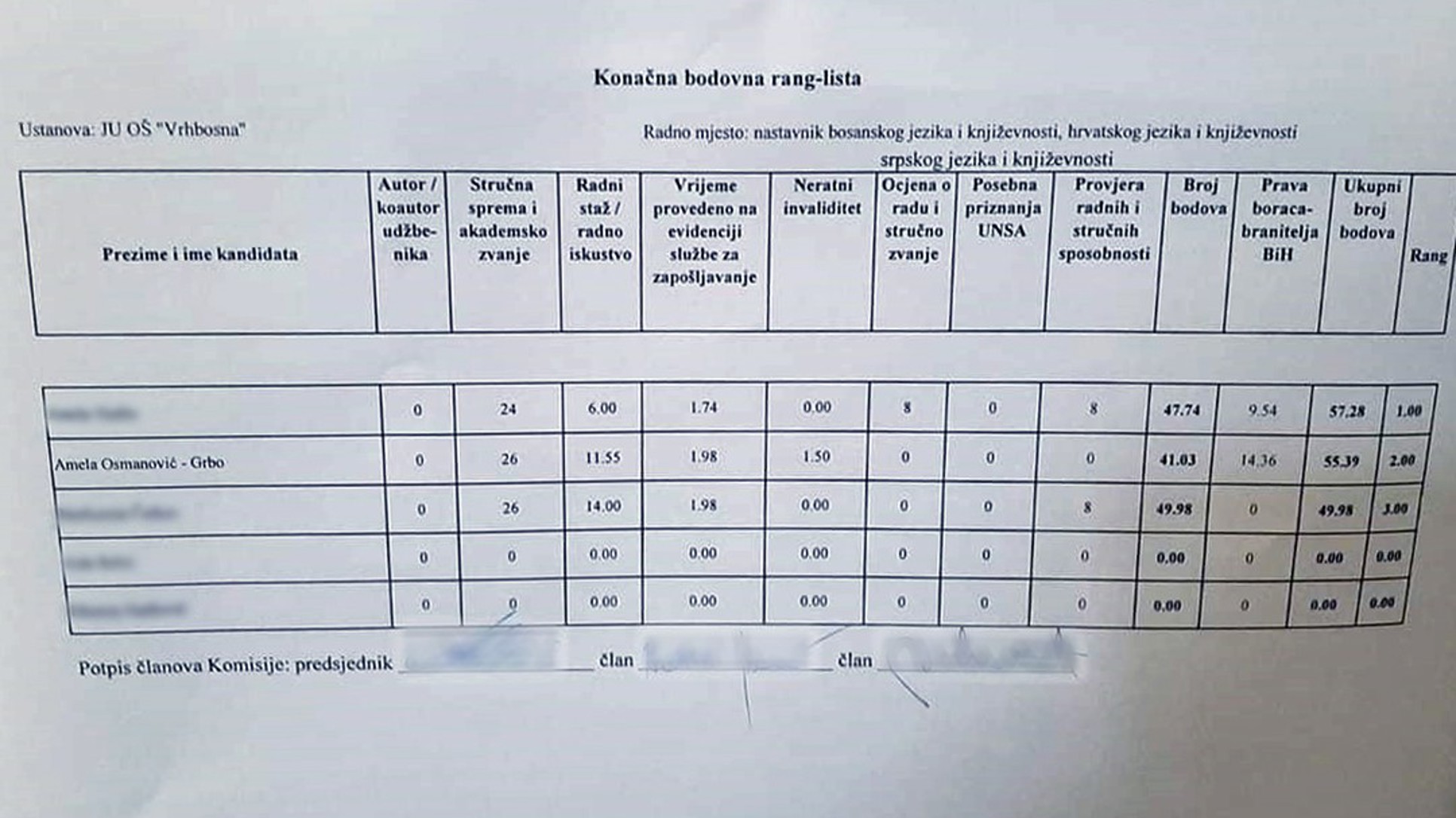
Ovo su dva od ukupno deset zadataka ovogodišnjeg maturskog testa. I ostalih osam su manje-više slični: hladni, precizni, apstraktni. Ispisani jezikom za koji nikoga nije briga zove li se bosanski, srpski ili hrvatski. Koliko ih je teško riješiti, toliko ih je lako ocijeniti. Ako je a, onda je 0,50 bodova, ako nije, onda je 0,0.
Nijedan od njih moja majka, nastavnica u penziji, ne bi znala riješiti. Ne bi ni većina njenih kolegica i kolega u zbornici. Ni većina roditelja. Možda su svi to jednom znali, ali su zaboravili, jer su im druge stvari zauzele mozak.
Moja majka je umrla prije 16 godina. Još čuvamo stvari koje su joj nešto značile, iako svako krečenje odnese ponešto. Ali ponekad odnekle ispadne neka sitnica, i zaboli. Recimo, ova cedulja, ispisana nekada lijepim, ali već umornim rukopisom:
190
grijanje 35,5
telefon 23
voda 5,5
struja 6
mačke 12
82,0
apoteka 40
dug 20
142
ulje 4
šećer 1
kafa 5
šampon 2
154
hljeb
190
154
=36
Eto, to je matematika koja ostane iza jednog života. Ne tvrdim da su oni maturski zadaci beskorisni: za nekoliko fakulteta to je neophodno znanje. Ali, matematika u osnovnoj i srednjoj školi morala bi biti šira od toga, drugačija, ljudskija. Možda bi se duže pamtila.
Zamišljam maturski test sa ceduljicom moje majke. I pitanja:
- Da li je račun na ceduljici ispravan?
- Šta je najveća stavka u računu, i zašto?
- 190 je iznos penzije u BiH, 2000. godine. Kolika je penzija danas? Šta sve jednom nastavniku u penziji treba za mjesec dana?
- Koliko košta hljeb za mjesec dana?
- Koliki je dug u računu, u procentima?
- Koliko od penzije ostaje za hranu, u procentima? Kolika bi trebala biti penzija da bi to bilo dovoljno?
- Koliko zrna kafe se može kupiti za 5 KM?
Itd.
Ne sjećam se, i ne mogu zamisliti da je nekada mojoj majci trebalo da zna ovo:
- Površina valjka je 28πcm2, a prečnik baze valjka je u razmjeri sa visinom kao 4 : 5.
Izračunaj:
- dužinu poluprečnika baze,
- zapreminu valjka.
Iako je to jednom znala, jer je bila odlična učenica. I svirala je lijepo klavir. Plela džempere, pisala pisma, pravila zimnice, krpila odjeću, samo nije išla redovno na preglede... heklala miljee, prala kupatilo, vezla goblene, pekla kolače i knedle sa šljivama... vukla cekere s pijace (da, imali smo i tatu). Ustajala je u 5, da bi skuhala ručak i pripremila doručak, prije nego u sedam ode na drugi posao. S kojeg, kad bi se vratila u jedan, nastavljala bi prvi: pranje prozora (koju površinu stakla žena opere u stanu, ako stan ima pet prozora, dimenzija xyz, a svaki prozor dva stakla?), usisavanje podova, peglanje posteljine, mljevenje kafe (ako je površina valjka mlina xyz, a prečnik baze u razmjeri s visinom x:z, izračunaj: koliko zrna kafe može stati u mlin, ako je zrno dimenzija xyz?)
Mislim, možda bešćutnost jednog društva, nesposobnost zajednice da prepozna nepravdu, tlačenje, privilegije... počinje, između ostalog, njenim poimanjem matematike u obrazovanju, gdje su sve njene veze s etikom pokidane u tvrdoj apstraktnosti. I možda onaj djetinji strah, od nje, čak i kada imaju petice, nema veze s brojevima, operacijama i formulama, nego s neljudskom hladnoćom krute pedagoške tradicije koju školska inercija odgaja kao vrlinu.